La primera pregunta que debemos plantearnos al iniciar la descripción de las soluciones a las ecuaciones que describen el cable lineal es: ¿qué tratamos de encontrar resolviendo estas ecuaciones? La respuesta a esta pregunta es: queremos encontrar parámetros medibles experimentalmente que nos permitan obtener los valores de los tres componentes del circuito equivalente que constituye el cable (Figura 1). Cuando lo pensamos bien encontramos que esto es verdaderamente notable, ya que con solamente tres parámetros (Ri, Rm y Cm) hemos construído un circuito equivalente que describe el comportamiento eléctrico de un gran número de células, aunque básicamente de un solo tipo, cilindros regulares largos. Las dificultades que tenemos para encontrar el valor de esos parámetros se deben a que sus propiedades se encuentran tan mezcladas que no pueden ser medidas directamente, por lo que tenemos que medir propiedades que resultan de la interacción de los tres componentes del circuito completo y de ahí extraer los valores de los parámetros individuales.
Una fuente común de confusión es la que se origina con el uso de las palabras "pasivo" o "lineal", en contraposición con "activo" o "no-lineal". Brevemente, por lineal entendemos que los componentes del circuito equivalente no cambian debido a la perturbación aplicada, lo que también puede expresarse diciendo que la resistencia se comporta ohmicamente, esto es, de acuerdo a la ley de Ohm. Recordemos que esta ley dice que el voltaje es función lineal de la corriente, con la resistencia como la constante de proporcionalidad. En los casos en los que la resistencia no es constante, las relaciones entre V y I no son lineales y a esto es a lo que llamamos un sistema no-lineal o activo (Figura 1)
Figura 1. Relaciones entre la corriente y el voltaje, típicas de las relaciones lineales o pasivas, y no-lineales o activas. A. La gráfica ilustra una relación I-V lineal, con una pendiente igual a 1/R. B. En esta gráfica la relación no es una línea recta, indicando que a cierto valor del voltaje la resistencia del sistema cambió. Relaciones como las de A son típicas de células inexcitables, mientras que aquellas como las de B se obtienen en celulas excitables.
La solución mas general de la ecuación del cable es la llamada "solución con la función error" y fue obtenida inicialmente por Hodgkin y Rushton (1946). La forma general de esta solución al aplicar un pulso en el intervalo 0<x<∞ es la siguiente:
![]()
donde,
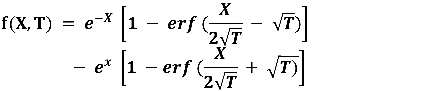
La función error proviene de la función de distribución normal o Gaussiana, que es dada por:
![]()
donde la integral de una de sus mitades (de 0 a x) es la función error (erf) definida por:
![]()
Estas dos funciones son graficadas en la Figura 2 y las hemos puesto juntas con el propósito de comparar sus formas y relaciones.
Figura 2. Gráfica de una mitad de la función de distribución normal [G(x)] y su integral, la función error [erf (x)].
Los cálculos numéricos a partir de la solución general de la ecuación del cable (ecuación 1) son largos y tediosos y actualmente no es necesario hacerlos a mano, ya que cualquier computadora, aún de las mas pequeñas, es capaz de resolver esas ecuaciones en pocos segundos. Por ello, lo que haremos ahora puede hacerse con facilidad y es que partiendo de algunas simplificaciones, resolveremos las ecuaciones que son de forma mas sencilla que la ecuación (1).
La ecuación general del cable se muestra abajo nuevamente:
![]()
Con el fin de resolver una forma simplificada de esta ecuación empezaremos por eliminar el término τ ∂Vx/ ∂t , lo que puede hacerse si suponemos que el sistema se encuentra en el estado estacionario, esto es, cuando ya no hay cambios del voltaje con respecto al tiempo. En estas condiciones tenemos,
![]()
Con esta suposición, la ecuación general del cable (arriba s/n) cambia a una forma que tiene validez solamente en el estado estacionario,
![]()
![]()
La solución de esta ecuación, independientemente de los valores que puedan llegar a tener los parámetros A y B, se parecerá a la gráfica que se muestra en la Figura 3.
Figura 3. Gráfica de la solución de la ecuación del cable durante el estado estacionario.
Como se muestra en la Figura 3, observando la suma de las dos exponenciales e iniciando de izquierda a derecha, la solución tendrá un valor numérico alto que dependerá de donde empezamos, disminuirá conforme la exponencial disminuye y posteriormente volverá a aumentar debido a la contribución de la otra exponencial. Sin embargo, el problema que esta solución representa para nosotros es bastante claro cuando la comparamos con los valores que esperaríamos que tuviera el voltaje a lo largo del cable.
Nosotros esperariamos que conforme la distancia desde el punto de inyección de corriente aumenta (+x) y una fracción de la corriente que fluye internamente (i i ) escapa a través de la membrana de cada segmento (i m), habrá menos corriente, de tal manera que en regiones lejanas al punto inyectado (formalmente en + ∞), no habrá mas corriente fluyendo en el interior del cilindro o a través de la membrana. Mas aún, ya que la corriente transmembranal disminuye conforme nos alejamos del punto donde fue inyectada, se producirá un cambio de voltaje cada vez menor en el circuito R || C que representa la membrana. Por lo tanto, conforme la distancia desde el punto de inyección de corriente aumenta, el voltaje Vm debe disminuir y finalmente llegar a cero.
Como lo que esperamos que suceda no es igual a la forma de la solución de la ecuación, debemos resolver este problema haciendo que la constante A sea igual a 0. Con esto, la ecuación solución se convierte en,
![]()
El valor de B puede obtenerse de la misma ecuación (7) si notamos que cuando x = 0, Vx = V0 y la sustitución de este valor en la ecuación nos da,
![]()
Hay dos parámetros que veremos mas abajo y caracterizan completamente las propiedades del cable: 1) la constante de espacio, y; 2) la constante de tiempo; sin embargo, debe quedar claro que aún caracterizando el cable no podemos obtener todavía los valores de los componentes del circuito. Ya que hay tres componentes en el circuito equivalente (Ri, Rm y Cm), necesitamos al menos tres ecuaciones para obtenerlos y para esto, haremos uso de las ecuaciones que describen la constante de espacio (λ) y la constante de tiempo (τ), y también de otro parámetro conocido como la resistencia de entrada (R0). La importancia de estas tres ecuaciones es que describen tres parámetros que podemos medir durante un experimento electrofisiológico.
Los parámetros medibles son,
![]()
y a partir de ellos podemos calcular que,
![]()
y obtener los valores específicos de los componentes de la membrana usando las conversiones descritas en la sección Unidades.
Rm = 2 π a rm y Cm = cm/2 π a
El valor de la constante de longitud puede ser obtenido a partir de la ecuación (8) haciendo x = λ. Entonces,
![]()
De esta manera, λ, llamada " longitud característica o constante de espacio", es aquel valor de x en el que Vx ha disminuído a 1/e (~37%) de su valor original (Vo) y, por supuesto, tiene unidades de longitud (cm). Su significado proviene del hecho de que proporciona una medida de la caída del voltaje transmembrana a lo largo del cable. Esta caída es producida porque en cada segmento del cable hay una fracción de la corriente fluyendo internamente que sale a través de la membrana, dejando menos corriente para el siguiente segmento.
Sin embargo, hay que recordar que este concepto de la constante de longitud se aplica solamente bajo ciertas condiciones (las suposiciones originales): 1) que la fibra sea homogénea en sus propiedades, de tal manera que se pueda aplicar el análisis del cable; 2) que la fibra sea de una longitud "infinita", o por lo menos mucho mas larga que su diámetro, y; 3) que la membrana (y el voltaje a través de ella) haya llegado a su estado estacionario. Posteriormente discutiremos algunas variaciones en relación a este último punto.
La constante de longitud del cable puede ser obtenida también de una manera gráfica si empezamos con la ecuación (8):
![]()
donde, tomando logaritmos naturales obtenemos:
![]()
Esta es la ecuación de una línea recta (y = - ax) y nos indica que si graficamos los parámetros V y x obtenidos experimentalmente, el recíproco de la pendiente de la línea obtenida será la constante de longitud. Este procedimiento se ilustra en la Figura 6.
Figura 6. Método gráfico para obtener la constante de longitud.
La constante de tiempo (τ) de la membrana puede ser obtenida considerando una célula representada adecuadamente por un solo elemento Rm||Cm del cable, tal como la de la Figura (2). En este caso, la corriente que cruza la membrana (im) será igual a la suma de la que fluye a través de la resistencia mas la que fluye en el capacitor, tal como lo describe la ecuación (6).
![]()
Ya que, de acuerdo a una definición previa, τm = rm cm, podemos reescribir la ecuación (6) como,
![]()
La solución a esta ecuación es:
![]()
de donde podemos obtener el valor de τ haciendo t = τ . Por lo tanto, τ es el tiempo al cual el voltaje transmembrana llega a una fracción (1-e-1) del valor final, lo que corresponde a aproximadamente 63% de im rm.
La constante de tiempo caracteriza el comportamiento temporal de los cambios de voltaje a través de la membrana; esto es, es una medida de cuan rápido se carga (o descarga) el capacitor de la membrana. Sin embargo, debemos mencionar que este análisis se aplica solamente a cambios de voltaje que tienen formas realmente exponenciales en el tiempo, lo que ocurre solamente para células que pueden ser representadas por un simple circuito equivalente que tiene una resistencia y un capacitor en paralelo.
Un método gráfico para obtener esta misma constante de tiempo utiliza la ecuación (15) que dice que la corriente total que cruza la membrana, es la suma de la corriente capacitiva mas la corriente resistiva. Esta ecuación es:
![]()
Esta ecuación está basada en un circuito equivalente donde la resistencia lineal que hemos usado hasta ahora ha sido sustituída por una no-lineal y a través de la cual fluye corriente iónica. Por lo tanto im = ic + iion.
Como también sabemos que iion = Vm/Rm, podemos reescribir la ecuación (15) como:
![]()
y si definimos V∞ = imRm, tendremos que,
![]()
La solución de la ecuación (20) es:
![]()
Ahora, cuando t = 0 y V = 0, resulta que K = ln Vi ; por lo tanto,
![]()
y rearreglando esta ecuación obtenemos:
![]()
de donde 1 - Vm/Vi = e -t / τ y multiplicando por V∞ resulta,
![]()
La ecuación (23) es de una línea recta que puede ser graficada de la siguinte manera:
Figura 7. Método para obtener la constante de tiempo (τ) de una membrana.
donde el recíproco de la pendiente es la constante de tiempo.
Cuando las características geométricas de una célula indican que su representación mas adecuada es la del cable, la constante de tiempo tiene un significado diferente. Para demostrar esto usaremos la solución general a la ecuación del cable, que es la siguiente:
![]()
donde f (X,T) es una función error tal que a una distancia x = 0 se convierte en f (0,T). Por lo tanto,
![]()
y ya que λ = √rmri podemos reescribir la ecuación (25) como,
![]()
y cuando t = τm tendremos que T = t/τm = 1
![]()
El valor numérico de esta función puede ser obtenido en las tablas apropiadas, donde encontramos que f (0,1) = 1.685 y haciendo la sustitución, obtenemos:
![]()
La diferencia con la constante de tiempo para funciones exponenciales, como la que obtuvimos a partir de una célula esférica, es que en este caso τ es aproximadamente 84% del valor máximo, en vez del 63% que encontramos anteriormente.
![]()
![]()
La solución de la ecuación del cable en el estado estacionario es:
![]()
Derivando esta ecuación con respecto a x obtenemos:
![]()
y sustityendo e (-x/λ) de (8) en la ecuación (13) resulta,
![]()
Una ecuación obtenida directamente del cable y que ya hemos usado anteriormente, es la siguiente:
![]()
y como a una, x = 0+, Vx = Vo y i i = io, por sustitución de estos parámetros y la ecuación (3) en la ecuación (14), obtenemos,
![]()
Ahora, recordemos que las conversiones entre valores por unidad de longitud y específicos son, rm=Rm/ 2 π a y ri=Ri/ πa2, por lo que sustituyendolos obtenemos:
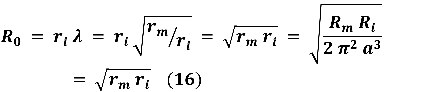
Este parámetro (Ro) se conoce como la "resistencia de entrada" de una mitad del cable y tiene unidades de resistencia (Ω). Sin embargo, si consideramos ambas mitades del cable la resistencia de entrada será 1/2 de la anterior, ya que las dos mitades se encontrarán en paralelo con respecto al electrodo de inyección de corriente y a tierra en el espacio extracelular.
![]()
La resistencia de entrada (Ro) nos indica el valor de resistencia encontrado por la corriente inyectada en x = 0; esto es, es la resistencia equivalente de todo el cable.
El uso correcto de este parámetro está restringido por las mismas suposiciones mencionadas para el uso de λ y una vez mas, que Vx sea medido a una distancia x = 0, o a una distancia suficientemente corta como para que podamos esperar que el valor Vx sea igual o muy semejante al que tendría en x = 0.