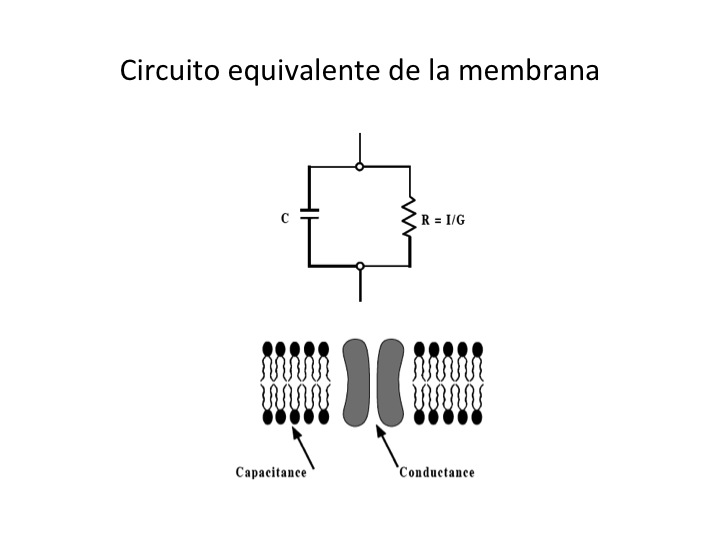

Como hemos visto, la membrana celular puede ser representada por un circuito equivalente que consiste en una resistencia y un capacitor en paralelo (Figura 1). Cada uno de esos elementos modela el comportamiento eléctrico de uno de los dos componentes principales de la membrana, la bicapa lipídica que la forma y las moléculas proteícas embebidas en ella que forman los canales iónicos. La bicapa lipídica se comporta eléctricamente como un capacitor y se representa como tal, y los canales iónicos se comportan y representan como una resistencia. Sin embargo, debemos recordar que el concepto de circuito equivalente de la membrana se desarrolló partiendo de una idealización, el comportamiento eléctrico de una célula esférica a la que se puede aplicar el concepto de simetría radial; esto es, la suposición de que el comportamiento eléctrico de toda la membrana celular es equivalente al de un área pequeña. Por otro lado y ya que muchas células cuya actividad eléctrica es de gran interés no son ni pequeñas ni esféricas, como por ejemplo los axones de las neuronas y las fibras musculares esqueléticas, el circuito equivalente de la membrana debe tomar en consideración la presencia de gradientes longitudinales de voltaje y para ello, en esta sección veremos un planteamiento sencillo del circuito equivalente que representa a las células alargadas. También podremos ver las definiciones de las unidades de resistencia y capacitancia de la membrana.
Una célula cuya longitud es mucho mayor que su diámetro puede representarse geométricamente como un cilindro regular. A su vez, ese cilindro puede imaginarse dividido en segmentos perpendiculares a su eje y de un grosor suficientemente pequeño como para poder decir que dentro de él no hay gradientes longitudinales o radiales de voltaje; esto es, cada segmento es isopotencial. Esta construcción es equivalente a la ilustrada en la Figura 2 y como podemos aplicar la simetría radial a cada segmento, estos pueden ser representados por el circuito equivalente de un área pequeña de la membrana como el de la Figura 1. La Figura 2 ilustra esta división de un cilindro regular en segmentos isopotenciales, cada uno representado a su vez por un circuito que tiene una resistencia y una capacitancia en paralelo (R||C), connectados entre si por la resistencia interna (Ri) y la resistencia externa (Ro), aunque frecuentemente esta es muy baja comparada con la del medio interior.
 |
 |
|---|---|
| Figura 1. Circuito equivalente de la membrana de una célula pequeña. | Figura 2. Circuito equivalente de la membrana de una célula alargada (cable). |
El estudio del comportamiento eléctrico de la célula alargada se hace encontrando los valores de los cuatro elementos del circuito equivalente que la prepresenta. Para esto, hay que formular la ecuación que describe el circuito y resolverla, como podemos ver mas abajo, pero antes analizaremos las unidades en que se expresan estos elementos. La resistencia de la membrana, la capacitancia de la membrana y la resistencia del medio interno son representados con dos letras cada una, una en mayúsculas y otra en minúsculas. Estas dos letras representan dos sistemas diferentes de unidades, los valores específicos (mayúsculas) y los valores por unidad de longitud (minúsculas). Supondremos que el volumen del medio externo es mucho mayor que el del interior de la célula y por ello no consideraremos esta resistencia, aunque se encuentra indicada en la Figura 2.
La resistencia interna de una célula corresponde a la resistividad o resistencia específica de su medio interno, compuesto principalmente por líquido. Así, la resistencia interna de una axón corresponde a la resistencia del axoplasma.
La resistividad tiene un símbolo, r, cuyas unidades son el Ω (Ohm) x centímetro (Ω.cm) y es la constante de proporcionalidad en la ecuación que describe la resistencia de un conductor.
R = r (l /A)
En esta ecuación R es la resistencia (Ω), r la resistividad, l la longitud del segmento y A el área de la sección transversal (cm2) del conductor.
La resistencia es una propiedad del conductor que depende de su tamaño, el material que lo compone y la temperatura, y su representación, el Ohm (Ω), es aquella resistencia a través de la cual un gradiente de voltaje de 1 Volt produce una corriente de 1 Amperio. La resistividad (r) es una característica de cada objeto o substancia y es la resistencia que un centímetro cúbico de esa substancia ofrecerá a una corriente aplicada perpendicularmente a dos de sus caras paralelas. Esa resistividad puede medirse como se ilustra en el diagrama de la figura 5, donde las placas, llamadas electrodos y hechas con una lámina fina de platino, tienen un área de 1 cm2 y están separadas por 1 cm, por lo que la cantidad de líquido contenido entre ellas es de 1 cm3. Como esta es la manera estándar de medir la resistividad de un líquido, está implícito en la forma en que hablamos acerca de esta medida. Expresamos la resistividad en términos de Ω-cm y sabemos que hemos medido 1 cm3 de líquido. Por ejemplo, la resistividad del medio interno del axón gigante del calamar es aproximadamente 35 Ω-cm, mientras que la de una fibra de músculo esquelético de rana, como el sartorio, es aproximadamente 200 Ω-cm.
Figura 5. Diagrama del aparato para medir la resistividad de un líquido.
La membrana que rodea una célula mantiene separados el contenido intracelular y el medio externo, y si encontraramos una célula suficientemente grande para tener 1 cm2 de esta membrana y la pudieramos aislara y mantener plana en líquido, se parecería al diagrama de la Figura 6.
Figura 6. Cálculo de la resistencia de la membrana
Si aplicamos un gradiente de voltaje de 1 Volt a ese cm2 de membrana, la corriente que lo atraviesa es llamada densidad de corriente y tendrá unidades de Amp/cm2. Por lo tanto y aplicando la ley de Ohm (R = V/I), la resistencia de esa membrana tendrá unidades de Ω-cm2. Esta es la que llamamos resistencia específica o resistividad de la membrana y para el axón gigante del calamar tiene un valor de aproximadamente 1000 Ω-cm2.
La corriente (ic) que fluye a través de un capacitor de capacitancia C cuando se le aplica una diferencia de potencial V, está descrita por la siguiente ecuación ,
ic = C dV/dt
donde, si en vez de corriente usamos densidad de corriente, con unidades de A/cm2, tenemos,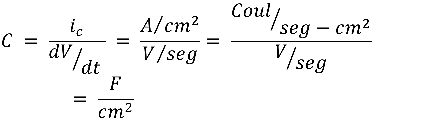
Estas son las unidades para la capacitancia específica de la membrana y para el axón gigante del calamar tiene un valor de aproximadamente 1 µF/cm2. Mas aún, como valores muy cercanos a ese han sido encontrados en todas aquellas membranas celulares que se han medido con precisión, se considera que este es el valor real de la capacitancia de 'todas' las membranas celulares.
Por conveniencia, se ha definido otro grupo de unidades que se usan en biofísica y electrofisiología, y son llamadas unidades por unidad de longitud. En ellas, la unidad de longitud es 1 cm y entra en las definiciones de los valores específicos dividiendo el volúmen o el área.
Ya que nos estaremos refiriendo contínuamente a una célula cilíndrica, es conveniente recordar algunos parámetros comunes a esta forma geométrica y que se ilustran en la Figura 7.
Figura 7. Parámetros geométricos de un cilindro regular
Como el medio interno de una célula es mayormente líquido, debe tener unidades de volumen (cm3), por lo que,
![]()
Para encontrar la resistencia por unidad de longitud dividimos el volúmen entre la longitud, de tal modo que,

lo que corresponde a las unidades de la resistencia interna por unidad de longitud.
Siguiendo un procedimiento similar al descrito arriba, podemos definir un parámetro que es la resistencia de membrana por unidad de longitud y ya que en este caso las unidades de membrana son las de área (cm2), tenemos que,
![]()
y en forma similar, dividiendo entre la unidad de longitud obtenemos,

Definimos un parámetro que es la capacitancia de la membrana por unidad de longitud y para ello multiplicamos por el área de membrana (cm2), ya que aquí la capacidad aumenta al aumentar el área.
![]()
Ahora, dividiendo área entre longitud tenemos,
![]()
Estas son las unidades de los parámetros con los que se describen las propiedades lineales de las células representadas por los circuitos equivalentes mostrados arriba y es conveniente recordarlos porque son usados frecuentemente.
Si se aplica un gradiente de voltaje a un conductor se inducirá una corriente a través del mismo. La constante de proporcionalidad entre esos dos parámetros, voltaje y corriente, es la resistencia del conductor, que se describe con la ley de Ohm. Esto puede esquematizarse en la siguiente forma.
Figura 8. Una resistencia lineal.
La expresión V = RI es la ley de Ohm, que formulada de esta manera implica que la resistencia es constante; esto es, la R es independiente de V. Cuando un conductor obedece la ley de Ohm se dice que es ohmico y en un circuito eléctrico una resistencia es un conductor ohmico. A este tipo de componentes, de los cuales la resistencia es un buen ejemplo, se les llama también lineales y si, por ejemplo, les aplicamos los tres tipos de voltaje ilustrados en la Figura 9, obtenemos las corrientes ilustradas también ahí.
Figura 9. Tres formas de ondas de voltaje aplicadas a una resistencia lineal producen corrientes cuyas formas de onda son iguales a las del voltaje.
Las corrientes que fluyen a través de una resistencia lineal tienen la misma forma de onda que la de los voltajes que les dan origen y esto se debe a que la resistencia es constante, independiente del voltaje aplicado a sus extremos. Esto es, las propiedades de la resistencia no cambian durante el tiempo que dura el estímulo.
En contraste con las resistencias, hay otros componentes cuyas propiedades si cambian, dependiendo de como cambia el voltaje aplicado a sus terminales. De todos esos componentes y debido a su relevancia en la descripción de las propiedades eléctricas de las membranas celulares, aquí solamente discutiremos el capacitor.
Un capacitor es un componente capáz de almacenar carga cuando se aplica una diferencia de potencial en sus extremos y debido a esto, la ecuación que lo describe y define su capacitancia es la siguiente.
Figura 10. Un capacitor y la ecuación que define la capacitancia.
Como el capacitor es capáz de almacenar carga (Q, en unidades de Coulombs) durante el tiempo que la corriente fluye a través de él, esa corriente (Ic) se define como la cantidad de carga almacenada durante un cierto periodo de tiempo; de donde,
![]()
que ya habiamos escrito como la ecuación 1.
Como cualquier otro sistema físico, un capacitor ofrece cierta oposición al paso de la corriente a través de él. Sin embargo, a diferencia de algunos otros componentes, esa oposición depende de que tan rápido cambia el voltaje que genera la corriente. Esto es parcialmente lo que la ecuación (1) dice, ya que si la velocidad del cambio de voltaje es muy grande, habrá una gran corriente capacitiva y si la velocidad de cambio de voltaje es cero, no habrá corriente fluyendo a través del capacitor. La propiedad que permite ese comportamiento del capacitor es también una oposición a la corriente, semejante a la resistencia del conductor, pero que en este caso se denomina 'reactancia' y como se refiere a un capacitor, se le llama 'reactancia capacitiva' (Xc); la ecuación que la describe es la siguiente,
![]() =
= ![]()
Nótese que en esta ecuación la oposición (reactancia) que encuentra la corriente es inversamente proporcional a la rapidéz (frecuencia, f) con que cambia la señal de voltaje, de tal modo que a altas frecuencia el capacitor ofrecerá poca oposición. En forma similar, la reactancia es inversamente proporcional a la capacitancia, lo que es fácil de entender, ya que los capacitores capaces de almacenar una gran carga tendrán menor reactancia al paso de corriente.
Como la reactancia capacitiva (Xc) depende de la frecuencia de la señal, es útil analizarla con ecuaciones que tomen en consideración esta característica (estas ecuaciones tienen números imaginarios, que se describen abajo). Sin embargo, ya que el circuito equivalente de una membrana celular contiene no solamente un capacitor, sino también una resistencia con propiedades lineales, tendremos que mezclar las propiedades de estos dos componentes. Esto se hace por medio de los números llamados complejos, que contienen una parte real y una parte imaginaria. De esta manera, tanto las propiedades lineales de la resistencia como las no-lineales del capacitor pueden ser analizadas conjuntamente.
En el caso del circuito equivalente de la membrana, donde la resistencia y el capacitor están en paralelo (Rm||Cm), la oposición combinada al flujo de corriente se llama 'impedancia', y puede ser definida formalmente como la relación entre la amplitud del voltaje complejo y la amplitud de la corriente compleja, donde la función de entrada es una corriente y la respuesta un voltaje.
Cuando los números complejos se obtienen de circuitos eléctricos se usa la siguiente nomenclatura, donde w es la frecuencia angular (w = 2 π f ),
jX(w) = R(w) + jX(w)
impedancia resistencia reactancia
o, si usamos las funciones recíprocas,
![]()
Y(jw) = G(w) + jB(w)
admitancia conductancia susceptancia
Por lo tanto, la impedancia puede ser descrita con la siguiente ecuación,
![]()
![]()
puede ser interpretada en forma similar a la ecuación que describe una resistencia simple (Figura 1), notando que el voltaje es proporcional a la corriente y donde el factor de proporcionalidad es la impedancia Z. Sin embargo, como la impedancia es un número complejo, no es inmediatamente claro cual sería la forma del voltaje que se obtendría en respuesta a una forma complicada en la corriente aplicada.