El flujo neto de un ión está dado por una expresión conocida como la ecuación de flujo de Nernst-Planck, que toma en consideración las fuerzas que actúan sobre el ión cuando, por ejemplo, cruza una membrana. Para llegar a la ecuación de Nernst-Planck primero analizaremos el concepto de flujo y desarrollaremos expresiones para los dos tipos de fuerzas que actúan sobre los iones, la fuerza química y el potencial eléctrico. Después, resolveremos la ecuación de Nernst-Planck para el caso del estado estacionario con el fin de llegar a una expresión que nos proporcione el voltaje transmembrana en función de las concentraciones iónicas. La ecuación de flujo será entonces convertida en una expresión para la corriente iónica total y que será expresada en dos formas, como permeabilidad y como conductancia. Ambas serán resueltas para el caso del estado estacionario, llegándose a expresiones que dan el potencial transmembrana en función de las permeabilidades iónicas (la ecuación de Goldman) y las conductancias. Una consideración final será el concepto de conductancia de la membrana, comparada con la permeabilidad de la membrana.
El flujo de una substancia desde una región a otra del espacio, puede ser expresada como la cantidad de substancia que cruza una unidad de área por unidad de tiempo. Este flujo está determinado por las fuerzas que actúan sobre las partículas, el número de partículas presentes y la velocidad adquirida por la partícula bajo la fuerza que la impulsa. Este último parámetro es llamado la "movilidad (μ)" y es definido como sigue:
μ = v / f (cm/seg dina)
La ecuación para el flujo será entoncesJ = c μ f (1)
Ya que estamos interesados en el flujo de partículas bajo la influencia de fuerzas químicas y/o electrostáticas, supondremos que estas son las únicas fuerzas actuantes y obtendremos expresiones para el flujo debido a cada una de ellas.
Si las únicas fuerzas actuando sobre las partículas fueran la eléctrica y la química, en un sistema cerrado a temperatura constante el cambio de energía libre (debido a la diferencia en estas fuerzas) puede expresarse como:
![]()
En esta ecuación, G es la energía libre de Gibbs, e la carga eléctrica, V el potencial eléctrico, n el número de moles de substancia y μ el potencial químico.
Para poder obtener expresiones para las fuerzas actuando sobre las partículas consideraremos, por ahora, que el potencial eléctrico es cero; esto es, nos referiremos a la difusión de no-electrolitos bajo el gradiente químico. Por lo tanto,
dG = n dμ
Si ahora dividimos entre N (el número de Avogadro) obtendremos la energía útil para el transporte de cada partícula,
![]()
El gradiente de energía por partícula, d u/N será la fuerza actuando sobre ellas y por lo tanto,
![]()
(suponiendo, por simplicidad, que la fuerza actúa solamente en una dimensión).
La dirección de la fuerza es aquella que produce la máxima disminución en u, y por lo tanto tiene el signo negativo. Si ahora introducimos esta ecuación en nuestra expresión para el flujo, llegaremos a:
![]()
![]()
![]()
![]()
![]()
La ecuación (5) dice que el flujo de las partículas debido a un gradiente de concentración es proporcional al negativo de ese gradiente, siendo la constante de proporcionalidad μ R T / N, que es llamado el coeficiente de difusión (D) y tiene unidades de cm 2/seg. Por lo tanto,
![]()
que es llamado 'coeficiente de difusión' (D) y tiene unidades de cm 2/seg. Por lo tanto,
![]()
Ahora, para el caso de una partícula a dos concentraciones constantes, pero diferentes a cada lado de una membrana, podemos escribir:
![]()
![]()
El cociente D/x se define como la 'permeabilidad' (P) de la membrana y tiene unidades de cm / seg. Usando este parámetro, la ecuación para el flujo en función de la permeabilidad de la membrana es la llamada "primera ley de difusión' de Fick, y es la siguiente:
![]()
En resumen, si la única fuerza actuando sobre las partículas es el gradiente químico, su flujo está dado por la ley de Fick.
Regresando a la expresión para la energía disponible para el transporte de partículas (ec. 2), ahora supondremos que la única fuerza actuando es el potencial eléctrico:
![]()
![]()
La energía disponible en un mol de substancia será:
![]()
![]()
![]()
![]()
![]()
Ahora el parámetro μ, definido como V/F, tiene, en el caso de iones, la siguiente definición, μe = v / E, donde E es el campo eléctrico. En este caso debemos usar la movilidad eléctrica y esta es dada por, μ = μe/e. Ahora, sustituyendo en la ecuación 10 tenemos que J = -cμez F/e N (dV/dx) y ya que eN = F, entonces J = -cμez (dV/dx). El coeficiente de difusión será ahora dado por μeRT / eN = μeRT / F, y la ecuación 10 se convierte en:
![]()
Si ahora suponemos que a ambos lados de la membrana existen potenciales diferentes, pero constantes, obtenemos:
![]()
![]()
![]()
Cuando ambas fuerzas, eléctrica y química, actúan sobre los iones, el flujo total estará dado por la suma de los flujos debidos a cada una de las fuerzas. En la ecuación (6) el coeficiente de difusión puede ser expresado en función de μe, de donde se obtiene D = μe RT/F. En la descripción siguiente no usaremos el subíndice "e" y por lo tanto D = μRT/F, ecuación que es conocida como la relación de Einstein. Entonces, tenemos que:
![]()
![]()
![]()
Para resolver la ecuación (14) vamos a suponer que el sistema está en equilibrio; esto es, que el flujo neto es cero. Entonces, si tenemos un ión permeable, donde D ≠ 0, la ecuación puede resolverse haciendo cero los términos entre paréntesis (equivalente a JTOTAL = 0). Esto resulta en:
![]()
![]()
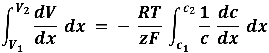
![]()
![]()
Una variante de la ecuación de Nernst-Planck que acabamos de obtener es la siguiente:
![]()
Consideremos ahora las unidades de las constantes de la ecuación. En el Sistema Internacional de Unidades (International System of Units, ISU) tenemos que,
R = constante de los gases 8.3143 Joules / °K mol
F = constante de Faraday 96,485 Coul / mol
T = temperatura absoluta ° K
(generalmente el valor de F se redondea a 96,500 para simplificar las operaciones).
La constante RT / zF tiene un valor de 0.02525 a 20 °C (293 °K) para una valencia z de +1 y si se cambian los logaritmos naturales a logaritmos en base 10, la ecuación (16) se convierte en:
![]()
![]()
donde las unidades de V son Volts. De manera que, en general y para tener el resultado en milivoltios, la ecuación se escribe como sigue:
![]()
Ahora, ¿qué nos dice la ecuación de Nernst?
Interpretando su significado encontramos que el potencial V es igual a una constante (RT / zF) multiplicada por el logaritmo natural (o el de base 10) de la relación entre las concentraciones iónicas dentro y fuera de la célula. Esto puede escribirse en términos mas simples, como:
![]()
Si la concentración no es uniforme, de tal manera que C2 ≠ C1, entonces ln C2/C1 ≠ ln 1(= 0) y por lo tanto, V ≠ 0, o sea que existe una diferencia de potencial.
En cambio, si se aplica una diferencia de potencial (V ≠ 0) tenemos que el ln C2/C1 ≠ 0 y por lo tanto C2 ≠ C1 y se habrá producido un gradiente de concentración.