La llamada ecuación de Nernst-Planck, que no vamos a derivar aquí, es la siguiente:
![]()
Las unidades de J en esta ecuación son cm2/seg y el flujo total es debido a la actuación de dos fuerzas, la química y la eléctrica. Esta ecuación puede ser expresada en función de la corriente total llevada por los iones y para hacer esto simplemente multiplicamos el flujo por la constante de Faraday (F) y llegamos a la siguiente ecuación:
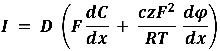
La ecuación tiene unidades de Coul/seg.cm2 o Amp/cm2, lo que indica que es una expresión para la corriente total por unidad de área y por lo tanto una densidad de corriente. Ahora, resolveremos esta ecuación para la corriente iónica y obtendremos el potencial de membrana en función de la permeabilidad de la membrana.
La corriente iónica fue dada por la ecuación de Nernst, que es la siguiente:
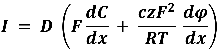
Ahora, usando D = µ RT/F y suponiendo que z = +1, la ecuación para la corriente iónica total se convierte en,
![]()
que puede ser resuelta integrando la corriente en todo el grosor de la membrana; la misma solución puede usarse para aniones (z = -1) cambiando solamente el signo. Esta integración no es difícil, pero en vez de hacer eso usaremos una simplificación que consiste en multiplicar ambos lados de la ecuación por el siguiente factor,
![]()
y obtenemos,
![]()
![]()
y es equivalente a los términos del lado derecho de la ecuación (2), por lo que igualándolos tenemos,
![]()
Cuando se integra en todo el grosor de la membrana es común suponer que dψ/dx es una constante, lo que es exacto para iones univalentes a concentraciones iguales en ambos lados de la membrana, aunque para sistemas biológicos es sólo correcta en forma aproximada. La ecuación resultante es llamada la 'ecuación del campo constante' (campo constante dψ/dx a través del grosor de la membrana). Otras constantes son, R, T, u, I.
Si ![]()
Por lo tanto, el voltaje en "x" será -V(x/d). La integración se lleva a cabo desde adentro hacia afuera, de manera que la corriente saliente será positiva (un ión positivo se moverá hacia afuera cuando dV/dx sea negativo). Esto produce las siguientes ecuaciones, en las cuales los subíndices "o" e "i" indican concentración externa e interna respectivamente.
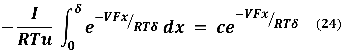
![]()
Rearreglando los términos obtenemos,
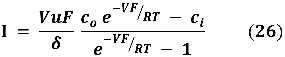
y recordando que P = D.x , tenemos,
![]() (integrado en toda la membrana)
(integrado en toda la membrana)
Por lo tanto, podemos escribir la ecuación como,
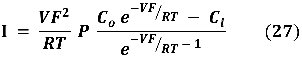
Esta ecuación puede ser aplicada directamente a los cationes Na+ y K+, y con un cambio de signo, también para el anión Cl-, como se muestra en las ecuaciones siguientes:
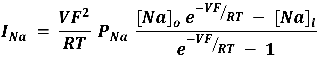
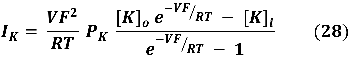
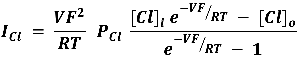
Estas tres ecuaciones para la corriente llevada por los iones Na+, K+ y Cl-, están expresadas en función de la permeabilidad de la membrana para cada uno de estos iones, tal como era nuestra intención original, pero si hay una corriente total debida a esos tres iones y la membrana es permeable a ellos, la suma de las contribuciones individuales estará dada por:
IT = INa + IK + ICl
Esta nueva expresión para la corriente total puede ser resuelta cuando el sistema se encuentra en el estado estacionario; esto es, cuando la corriente total es cero (el potencial V es una constante) y en este caso llegamos a la ecuación de Goldman (1943), también llamada ecuación de Goldman-Hodgkin-Katz (GHK). La corriente total (IT) es dada arriba y sustituyendo, tenemos:
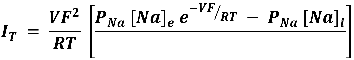
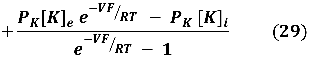
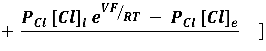
Si hacemos IT = 0, entonces,
![]()
![]()
y por lo tanto,
![]()
donde, tomando logarítmos naturales a ambos lados, llegamos a la ecuación de Goldman-Hodgkin y Katz, que es:
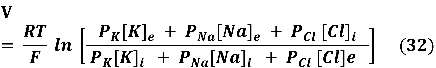
Esta ecuación nos proporciona el potencial de membrana en el estado estacionario en función de las permeabilidades y concentraciones de los iones.
Una simulación de los resultados obtenidos usando la ecuación de Goldman, Hodgkin y Katz, puede encontrarse aquí.
Cuando seleccione la simulación aparecerá un recuadro; por favor, espere unos segundos a que vea un letrero que dice "Adobe Flash Player Security" y seleccione "OK". Haga el recuadro del tamaño que guste, seleccionelo y aparecerá la pantalla con la simulación. En ella que puede seleccionar "Nernst", escoger uno de los iones (K, Na, Cl) y cambiar las concentraciones interna y/o externa para ver el valor del potencial de equilibrio. También puede seleccionar Goldman y cambiar las concentraciones de los mismos iones para ver el potencial de membrana.