EL COMPORTAMIENTO ELECTRICO DE LA MEMBRANA CELULAR

Una introducción a la biofísica de membranas de células excitables

I. INTRODUCCION

La descripción del comportamiento eléctrico del plasmalema o membrana celular, se basa en representar sus propiedades eléctricas con un circuito eléctrico equivalente y el descubrimiento de estas propiedades, así como el desarrollo del concepto de un circuito equivalente, fueron tema de estudio de numerosos investigadores durante años. Sin embargo, el primer paso fue la demostración de que todas las células están rodeadas por una membrana, la que fue hecha usando métodos electrofisiológicos.

La primera demostración de que la conductancia de un medio conteniendo células disminuye cuando la concentración de células aumenta fué hecha en 1899 por Steward, quien encontró que las células vivas tienen una resistencia eléctrica mayor que la del medio que las rodea. También observó que si las células eran destruídas con saponina, la conductancia del medio se hacía independiente de la concentración de células destruídas, por lo que llegó a la conclusión de que la resistencia eléctrica estaba localizada en la membrana.

La presencia de una capacitancia en la membrana celular fue demostrada por Rudolf Höber (1910), quien la estudió aplicando corriente alterna a suspensiones de diferentes células y encontró que cuando la frecuencia de la corriente aplicada era alta, la impedancia de la membrana era baja, ya sea que las células estuvieran intactas o destruídas. En cambio, cuando la frecuencia de la corriente era baja, la resistencia de un medio conteniendo células destruídas también era baja, mientras que la de un medio conteniendo células intactas era alta.

Posteriormente, alrededor de 1925, Hugo Fricke inició estudios con suspensiones de glóbulos rojos (eritrocitos) para medir la capacitancia de la membrana. Sus mediciones de la impedancia de esas células le permitieron calcular un valor de 0.81 µF/cm² para la capacitancia de la membrana, el cual, suponiendo una constante dieléctrica de 3 (igual a la del aceite), le daba un valor de 3.3 nm para el grosor de la membrana. Estos experimentos son descritos con detalle por Kenneth S. Cole (1966), quien continuó los experimentos de Fricke, estudiando en forma semejante una gran variedad de células y como consecuencia actualmente se considera que el valor de 1 µF/cm² para la capacitancia de la membrana es casi una constante biofísica.

Entre los experimentos clásicos en el estudio de la membrana celular se encuentran también los de Evert Gorter y Grendel (1925), quienes destilaron los lípidos de un número conocido de eritrocitos, encontrando que el área de la monocapa que obtenían era aproximadamente el doble de la superficie celular total. Su interpretación de esos resultados es aún válida, que la membrana está constituída por una bicapa de lípidos, pero fue una conclusión impresionante para aquella época. Así, todos esos experimentos y muchos otros demostraron la presencia y el valor de una capacitancia en la membrana celular.

La presencia de una resistencia eléctrica en la membrana celular fue establecida por medio de experimentos similares a los anteriores, conducidos por Fricke y Morse (1925). Estos experimentos fueron hechos con suspensiones de eritrocitos a los que aplicaron corriente alterna a varias frecuencias y fueron seguidos por células aisladas (huevecillos de los equinodermos Arbacia e Hippone, estrella de mar Asterios, grillos y axones gigantes de calamar), suspensiones de eritrocitos y tejidos (piel de rana, diafragma de gato, células cultivadas de músculo cardíaco de embriones de rata, músculo esquelético de rana), hasta llegar finalmente a los registros intracelulares en el axón gigante del calamar (Hodgkin y Huxley, 1939; Curtis y Cole, 1940).

Ya para mediados del siglo XX, Cole (1940) empezó a hacer mediciones internas del potencial de reposo y del potencial de acción con pipetas intracelulares llenas de KCl (Hodgkin y Huxley, 1939; Curtis y Cole, 1940). En estos experimentos y después de corregir los errores debido a los potenciales de unión líquida, obtuvo valores de aproximadamente -61 mV para el potencial de la membrana en reposo, mientras el potencial de acción promediaba 110 mV en amplitud. Con esos datos Cole encontró que la membrana tenía que invertir su polaridad durante el potencial de acción, pero como al sustituír el agua de mar con dextrosa isotónica su amplitud no cambiaba, concluyó que tal vez la inversión era debida a un efecto de resonancia ocasionado por una capacitancia (1 µF/cm²) y una inductancia (0.2 H/cm²) en la membrana. Como la inductancia ya había sido propuesta y utilizada anteriormente para explicar los resultados experimentales obtenidos durante las mediciones de la impedancia transversal de los axones gigantes (Cole y Baker, 1941), no le fue difícil aceptar que era el factor mas importante.

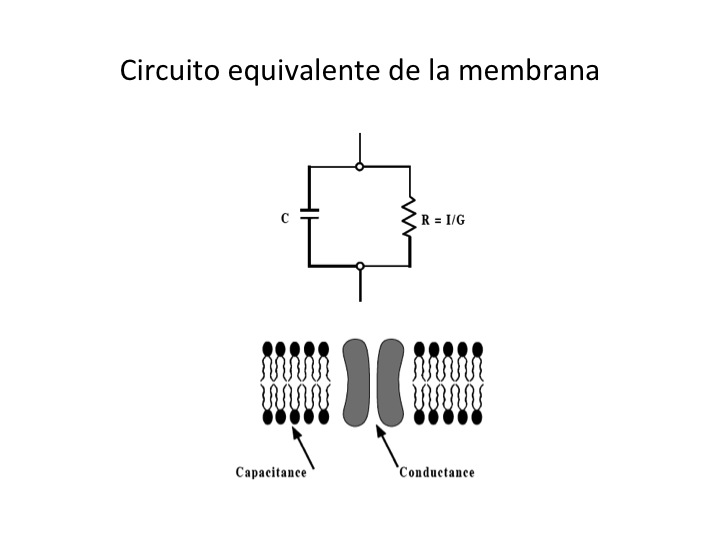
Por lo tanto, el circuito equivalente que Cole consideró inicialmente como una representación de la membrana contenía una inductancia, un componente que lo fascinó durante muchos años. Sin embargo, para 1947 lo abandonó y correctamente atribuyó el comportamiento inductivo a una consecuencia de las características no-lineales de la membrana. Así, el circuito equivalente usado actualmente para el estudio de las propiedades eléctricas de la membrana celular tiene solamente dos componentes en paralelo, resistencia y capacitancia, como se muestra en la Figura 1.

Fig. 1. Circuito eléctrico equivalente de la membrana. Los medios conductores interno y externo separados por la bicapa lipídica (dieléctrico) están representados por las placas del capacitor, mientras los canales iónicos para el sodio y el potasio lo están por la resistencia.

El circuito eléctrico equivalente (Figura 1) usado para el estudio del comportamiento eléctrico de la membrana celular se basa en las siguientes simplificaciones. Supongamos que la célula tiene una geometría semejante a la de una esfera como la que se muestra en la Figura 2A, donde la superficie corresponde a una membrana homogénea; esto es, con características similares en todos los puntos.

Si dividimos la esfera en dos mitades, cada una de ellas será idéntica a la otra. Después, cualquiera de esas mitades puede ser dividida en rebanadas de igual grosor y cada una de ellas será igual a cualquier otra, con una membrana y un medio interno. Por lo tanto, usaremos la primera rebanada, que tiene un diámetro igual al diámetro de la esfera. La vista frontal de esa rebanada se encuentra en la Figura 2C y en ese círculo ambas mitades son iguales, de manera que podemos considerar sólo una de ellas. En forma parecida, podemos ir dividiendo las fracciones en mitades y eliminando una de ellas, ya que ambas serían iguales y la membrana tendría propiedades semejantes. La única diferencia entre las diferentes fracciones de círculo que hemos obtenido es el área de membrana, que disminuye conforme la fracción se hace menor. Para corregir ese efecto podemos aumentar proporcionalmente las propiedades de los pequeños pedazos de membrana, de tal manera que un pequeño segmento describa las propiedades del área total de membrana de la esfera original. Esta reducción puede hacerse porque una esfera tiene la propiedad de 'simetría radial'. Recordemos que se dice que algo tiene simetría radial cuando puede ser dividido en mitades similares en cualquier plano que contenga el eje principal y esto es lo que ocurre con numerosos animales, como equinodermos (estrellas de mar), esponjas, medusas, etc.

Figura 2. Parámetros característicos de la simetría radial de una esfera.

En esa forma llegamos a la consideración de que una laminilla sumamente fina obtenida a partir de la esfera original puede representar todas las propiedades de la membrana. Como las propiedades de la membrana que nos interesan en este momento son solamente dos, su resistencia y su capacitancia eléctrica, estas propiedades deben estar contenidas en la membrana de la fracción de círculo con la que describimos la célula y que se muestra en la Figura 3.

Figura 3. Fragmento de membrana resultado de la reducción debida a la simetría radial de una esfera y el circuito equivalente que la representa.

Si consideramos que el diámetro del círculo en la Figura 2, que lo es a su vez de la esfera inicial, no es muy grande (menos de 1,000 µm), podemos suponer que no hay caídas de voltaje radiales y por tanto el voltaje en un punto cualquiera (V_i) será representativo del voltaje de cualquier otro punto en el interior. En forma semejante, si suponemos que el volúmen en el que se encuentra la esfera inicial es muy grande, o sea, que la resistencia del medio externo es muy baja comparada con la del medio interno, podemos suponer que no habrá caídas radiales de voltaje y por tanto el voltaje en el punto inmediatamente fuera de la membrana (V_e) es representativo del voltaje en cualquiera de las regiones externas del círculo. Así, por medio de un circuito equivalente que contiene una resistencia y un capacitor en paralelo, arribamos a la representación de las propiedades eléctricas de una célula esférica.

Tabla I-1. Valores de algunos dieléctricos, entre ellos la membrana celular. La intensidad dieléctrica es el máximo gradiente de potencial que puede existir antes que se produzca un rompimiento eléctrico (el de la membrana fue calculado con una diferencia de potencial de 200 mV).

Ahora describiremos en forma simple las regiones de la membrana a las que se adjudican las propiedades eléctricas que estamos considerando. Recordemos que la membrana celular está formada por una doble capa de lípidos (bicapa con un grosor aproximado de 6 nm), que estas son moléculas con una región polar (hidrofílica) y una no polar (hidrofóbica), y que se encuentran arregladas de tal forma que las regiones hidrofílicas enfrentan los medios intra- y extracelular (Figura 3). Debido a que la zona intermedia de la bicapa no es polar (hidrofóbica) no permite el paso de moléculas cargadas eléctricamente y por lo tanto actúa como un aislante con una constante dieléctrica de aproximadamente 3 (Tabla I-1). Así, la capacitancia está asociada con una separación de cargas producida por la bicapa de lípidos. La Tabla I-1 contiene las constantes dieléctricas de varios materiales, entre los que se encuentra una membrana celular (ver más adelante) y donde puede verse que es un buen aislante.

Figura I-3. Diagrama que ilustra una fracción de la membrana representando el total de la membrana de una célula esférica. El diagrama de la derecha muestra la doble capa de lípidos (base morfológica de la capacitancia) con sus regiones polares como pequeños círculos y las no-polares como prolongaciones saliendo de los círculos. El diagrama muestra además dos canales (uno de ellos seccionado) por que cruzan la membrana los iones. La suma de las resistencias individuales de todos los canales de la membrana constituye la resistencia total de la membrana.

En la bicapa lipídica se encuentran grandes proteinas, algunas de las cuales son los "canales iónicos", que podemos imaginar como 'tubos' pequeños con un diámetro menor de 1 nm y una longitud de cerca de 7 nm. Cuando estos canales están abiertos comunican los medios interno y externo de la célula. Su densidad es relativamente baja, de unos 500-5,000 canales por µm² de superficie de membrana y como están llenos de un materia hidrofílico (quizá agua misma), cuando están abiertos forman el camino por el cual los iones cruzan la membrana. Ese flujo de iones es la corriente eléctrica y la oposición que presentan los canales es la propiedad que llamamos resistencia. Así, como los canales son muy pequeños, cada uno de ellos tiene una resistencia muy alta (5,000-10,000 MΩ), pero como hay muchos de ellos en paralelo, la resistencia total de la membrana es reposo es baja, de 1-10 KΩ cm².

Por ejemplo, si cada canal tuviera una resistencia de 20x10⁹Ω (g = 50 pS) y en 1 cm² de membrana hubiera 2x10⁶ canales, la resistencia total 'específica' de este cm² de membrana sería de 20 KΩ.cm², un valor comúnmente encontrado en células de diferentes tejidos.

Las unidades usadas para describir los componentes del circuito equivalente de la membrana pueden encontrarse aquí, Unidades.